Need the area of a trapezoid right now? You’re in the right place. This guide walks you through our Area of a Trapezoid Calculator, shows the formulas behind it, and helps you avoid the usual mistakes. You’ll also see step-by-step examples, unit tips, and use cases. By the time you’re done you’ll feel confident calculating areas for class, design, or the jobsite.
We’ll keep the math friendly and the language plain. You’ll get clear headings, short paragraphs, and skimmable lists. Most of all you’ll get answers—quickly.
How to use the Area of a Trapezoid Calculator (60-second guide)
- Enter the two bases
aandb. These are the top and bottom parallel sides. Use any unit you like. - Enter the height
h. That’s the perpendicular distance between the bases. - Click or tab away. The calculator shows the area instantly in your chosen area unit.
- Optionally add the slanted sides
canddto get the perimeter and all four angles. - Use the Copy button to grab results or the Share button to send a prefilled link to a teammate.
Tip: If the bases use centimeters and the height uses inches the calculator converts on the fly. No manual unit juggling.
What a trapezoid is (and what it isn’t)
A trapezoid is a quadrilateral with exactly one pair of parallel sides. Many regions call the same shape a trapezium. The parallel sides are the bases a and b. The other two sides are legs c and d. The height h drops straight from one base to the other at a right angle.
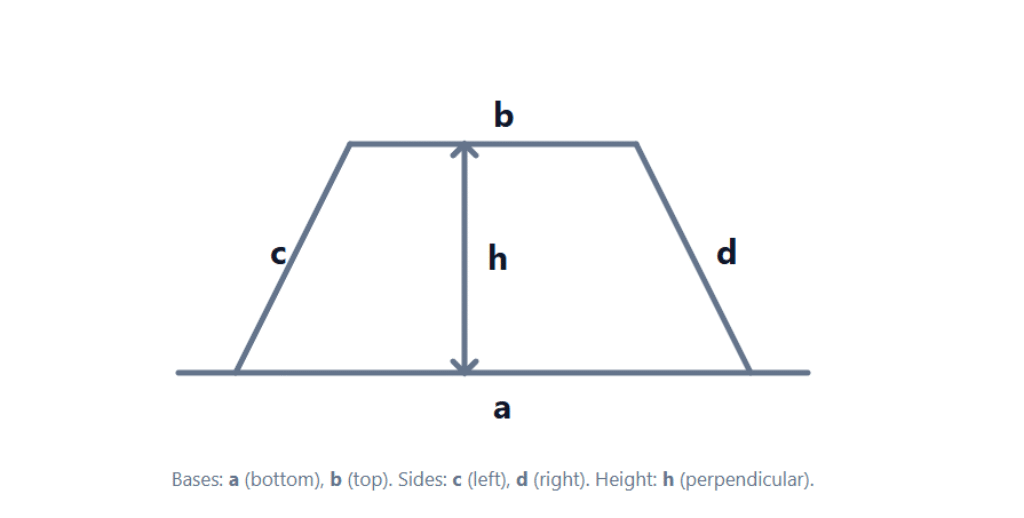
a and b are parallel; height h is perpendicular; legs are c and d.Area of a trapezoid formula (the one you’ll actually use)
The core formula is simple:
Area A = (a + b) × h ÷ 2
a= length of the first baseb= length of the second baseh= height (perpendicular distance)
It’s the average of the bases times the height. That’s it. If you remember one thing remember that.
When the formula simplifies
- Parallelogram case: if
a = bthenA = a × h. A parallelogram is just a trapezoid with equal bases. - Right trapezoid: one leg is perpendicular to the bases. The area formula doesn’t change but height equals that right leg.
- Isosceles trapezoid: legs are equal; area still uses the same formula.
Worked examples you can copy
Example 1: basic area
Given: a = 12 cm, b = 8 cm, h = 5 cm.
Compute: A = (12 + 8) × 5 ÷ 2 = 20 × 5 ÷ 2 = 50 cm².
Example 2: find the height from area
Sometimes you know the area from drawings or requirements. Solve for h quickly.
Given: A = 72 m², a = 10 m, b = 14 m.
Height: h = 2A ÷ (a + b) = 144 ÷ 24 = 6 m.
Example 3: mixing units
Given: a = 40 in, b = 2 ft, h = 0.5 yd.
Convert bases to inches: b = 24 in. Convert height to inches: h = 18 in.
Area: (40 + 24) × 18 ÷ 2 = 64 × 9 = 576 in². The calculator does these conversions automatically.
Perimeter of a trapezoid (optional in the calculator)
If you enter the legs c and d the calculator shows the perimeter:
P = a + b + c + d
That’s handy when you price edging, trim, or railing. Use the unit dropdown to switch between meters, feet, or miles without manual math.
Angle finder (also optional)
Angles help when you cut fascia, stair stringers, or sheet goods. The calculator gives all four interior angles when you have the bases, height, and both legs. It also checks consistency for you.
- Left bottom angle
α = arctan(h / xleft) - Left top angle
β = 180° − α - Right bottom angle
δ = arctan(h / xright) - Right top angle
γ = 180° − δ
Here xleft = √(c² − h²) and xright = √(d² − h²). These are the horizontal “run” parts of the slanted legs.
Guardrail: If |a − b| ≠ xleft + xright you’ll see a warning. That message flags inputs that can’t form a valid trapezoid.
Real-world uses where a trapezoid pops up
- Roofing and siding: Hip ends and gables often cut into trapezoidal panels. Area drives material takeoff.
- Landscaping: Beds and planters follow fences or sidewalks at odd angles. Trapezoids give fast mulch estimates.
- Civil engineering: Road shoulders and channels use trapezoidal cross sections. Area feeds flow and fill calculations.
- Woodworking: Tabletops, shelves, and inlays use clipped corners that create trapezoids.
- Graphic design: Banners, tickets, and labels use trapezoid shapes for emphasis.
If you work with slopes you may also like our Slope Percentage Calculator. For fraction-heavy drawings try the Simplify Fractions Calculator.
Common mistakes and how to fix them
- Using a slanted side as height. Height must be perpendicular to both bases. If you drop a vertical from the top base to the bottom base you’ll see it clearly.
- Mixing units. Keep bases and height in the same length unit. The calculator converts automatically but you still want your drawings consistent.
- Forgetting averages. You don’t multiply just one base by height. Take the average:
(a + b) ÷ 2. - Impossible inputs. Legs can’t be shorter than the height. The warning catches those cases.
Formulas at a glance
| Quantity | Formula | Given |
|---|---|---|
| Area | A = (a + b) × h ÷ 2 |
a, b, h |
| Height from area | h = 2A ÷ (a + b) |
A, a, b |
| Perimeter | P = a + b + c + d |
a, b, c, d |
| Horizontal offsets | xleft = √(c² − h²), xright = √(d² − h²) |
c, d, h |
| Consistency check | |a − b| = xleft + xright |
a, b, c, d, h |
Frequently asked questions (clear and concise)
What is the area of a trapezoid?
It’s the space inside the shape. Multiply the average of the two bases by the height. Use A = (a + b) × h ÷ 2. Keep units consistent.
Can I find height if I only know area and the bases?
Yes. Rearrange the formula to h = 2A ÷ (a + b). The calculator includes this scenario. Enter area and both bases then read the height.
What’s the difference between a trapezoid and a trapezium?
In American English a trapezoid has one pair of parallel sides. In British English that shape is a trapezium. Both terms refer to the same calculator inputs here.
Do I need the legs to get area?
No. The legs matter for perimeter and angles only. Area uses just the bases and the height.
Does the calculator support degrees and radians?
Yes. Choose degrees, radians, gradians, turns, milliradians, microradians, or multiples of π from the angle unit dropdown.
Step-by-step: from sketch to answer
- Sketch the trapezoid. Label the longer base
aand the shorter baseb. Draw the height straight down. - Measure. Capture
a,b, andhin the same unit. If you work from blueprints read the scale carefully. - Enter values. Use the calculator’s fields for the bases and height. The area updates automatically.
- Switch units if needed. Change the area unit to get
cm²,m²,ft²,yd², hectares, or acres. - Add legs for extras. Enter
canddto get perimeter and angles. Watch for the consistency message if something looks off. - Copy, share, and save. Use the buttons under each result to keep your work moving.
Why this calculator saves you time
- Unit smart: Inputs mix units without friction. You can type feet for one side and meters for another. The calculator harmonizes them.
- One-screen design: Results sit next to the inputs. No page reload or hidden steps.
- Shareable links: Click Share and send a prefilled URL to a coworker who can verify the same numbers.
- Consistency guard: The geometry check catches impossible trapezoids so estimates don’t drift.
- Bonus outputs: Perimeter and angle set help when you move from math to material and cuts.
Unit tips that prevent headaches
- Match systems on the same drawing. Stick with metric or imperial throughout a plan set.
- Square units sneak up on you. Double the length doesn’t just double the area. It quadruples it. Keep that in mind when scaling.
- Square feet to square yards: divide by 9. Square inches to square feet: divide by 144. Square meters to hectares: divide by 10,000.
- Need help visualizing sizes? One acre equals roughly 43,560 ft². A soccer field runs close to 1.76 acres depending on the standard. These comparisons keep results grounded.
For the Curious Minds
How do you calculate the area of a trapezoid?
Answer: Add the two bases, divide by two to get the average, then multiply by the height. Use A = (a + b) × h ÷ 2. Measure height perpendicular to the bases.
What is the formula for the height of a trapezoid?
Answer: Rearrange the area formula to h = 2A ÷ (a + b). Provide area and both base lengths to solve for height directly.
Does a trapezoid’s area depend on the slanted sides?
Answer: No. Area depends only on the two bases and the height. The legs affect perimeter and angles not area.
Behind the formula: a quick intuition
Imagine sliding triangles off the ends of a trapezoid and packing them into the middle. The shape becomes a rectangle whose width equals the average of the two bases and whose height equals the original height. That’s why the formula uses (a + b) ÷ 2.
Where to learn more
- Refresh trapezoid definitions and properties with Wikipedia’s overview.
- Watch a short geometry refresher on area from Khan Academy.
- Check SI unit guidance in the NIST SI pages.
Calculate trapezoid area with confidence
You don’t need a textbook to find the area of a trapezoid. You need the right inputs and a clean interface. Enter bases a and b with the height h, and the Area of a Trapezoid Calculator gives you the answer on the spot. Add the legs if you want perimeter and angles. Copy the results. Share the link. Move on with your project.
Bookmark this page and come back anytime your plan, panel, or patch of ground turns into a trapezoid. The calculator will be here when you need it.
